Univers Gémellaires :
Le Modèle Janus
3.4
Photo de Drift Shutterbug sur Pexels.
Cet univers d’antimatière à masse négative (à ne pas confondre avec l’antimatière à masse positive créée en laboratoire dans notre univers) n’a pas le même contenu, et ne connaît pas les mêmes conditions, ni les mêmes lois physiques que notre univers de matière positive ! Par exemple, la lumière ne s’y déplace pas de la même façon.
En effet, l’une des particularités – et non des moindres – du Modèle Janus est de proposer l’hypothèse de variations conjointes de toutes les constantes de la physique : vitesse de la lumière, constante gravitationnelle, constante de Planck, charge électrique unitaire, masse, et perméabilité magnétique du vide. Jean-Pierre Petit rajoute également deux « facteurs d’échelle » (deux variables) aux équations de la physique, une première concernant l’espace, une deuxième concernant le temps.
Prenons l’exemple de la vitesse de la lumière.
La lumière est présentée dans le modèle de la Relativité Générale comme une constante universelle. Dans le modèle Janus, on va plutôt considérer que sa façon de se déplacer dépend de l’Univers dans lequel elle se trouve, et des conditions, comme du contenu, de cet univers. À deux univers différents, deux contenus différents, deux métriques différentes (nous allons y revenir), et deux Physiques différentes ! La lumière ne circulera donc pas de la même manière dans l’univers d’antimatière, et ne subira pas les mêmes limitations de vitesse qu’elle connaît dans l’univers positif !
Mais quel rapport avec les voyages interstellaires ?
Voici la réponse de Jean-Pierre Petit, telle que donnée dans l’interview rapportée par la vidéo du Précepteur (en page 1, et à 36:56) :
« Vous avez des photons d’énergie positive qui ne peuvent pas aller plus vite que 300 000 kilomètres par seconde, mais les photons d’énergie négative ne peuvent pas aller plus vite que 3 000 000 de kilomètres par seconde, il y a facteur 10 ! […] Si tout d’un coup, vous avez un véhicule qui arrive à inverser sa masse, eh bien il peut franchir des distances, et à ce moment-là, il a une limitation de vitesse qui lui laisse une plage beaucoup plus large, puisqu’elle est dix fois plus grande, et les distances sont raccourcies d’un facteur 100. Donc il gagne un facteur 1000 sur la durée, donc les voyages interstellaires deviennent faisables ».
Ceci est d’autant plus vrai si l’on considère que l’Univers Jumeau est régi selon une métrique différente du nôtre. Une métrique, c’est une façon de calculer la longueur, dans un espace où les points sont définis par des coordonnées.
Or, selon Jean-Pierre Petit : « A partir d’un Big Bang les deux populations entrent en expansion. Mais ce processus s’avère instable, une des populations prenant le pas sur l’autre. Chacune possède son propre jeu de « constantes variables ». À cela, il faut ajouter des « jauges d’espace », ou « mesures des distances », qui diffèrent. […] L’expansion est plus prononcée dans une des populations ( notre secteur d’univers ). » >>
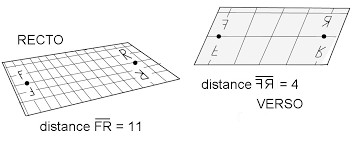
« Ici intervient ce qui est le plus difficile à envisager : qu’entre deux points de l’espace il puisse exister deux distances différentes. On peut essayer de suggérer cela en imaginant doter une surface de deux quadrillages, l’un inscrit sur le recto, et l’autre sur le verso. Faisons deux trous avec une épingle, matérialisant deux points distants F et R. On peut
imaginer qu’on puisse mesurer différemment la distance qui les sépare, selon qu’on se réfère au quadrillage figurant sur le recto ou sur celui figurant sur le verso. »
Nous observons l’inversion des points R et F sur le verso, les lettres les figurant sur la surface du papier étant « orientables ». Ceci nous rappelle très logiquement le caractère énantiomorphe des deux Univers (symétriques « en miroir »).
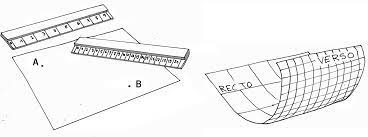
L’idée du voyage interstellaire est de passer du recto au verso de l’hypersurface espace-temps. De son endroit à son envers, de l’autre côté du miroir en quelque sorte, afin de bénéficier de sa métrique différente.
Le Modèle Janus permet donc notamment d’envisager de raccourcir les distances entre deux points de l’espace éloigné, non pas en dépassant la vitesse de la lumière, mais en changeant d’espace, de la même façon que l’on peut effectuer un même trajet dans deux milieux aussi différents que l’air ou l’eau, à des vitesses différentes, en raison de conditions différentes !

