Univers Gémellaires :
Le Modèle Janus
2.4
Photo de Drift Shutterbug sur Pexels.
Qu’entend-on par « antimatière à masse négative » ?
Une masse est une quantité de matière. Tout le monde comprend ce que peut être une quantité de matière positive, que l’on peut exprimer au travers de nombres : + 1, + 2, etc. Mais comment comprendre l’antimatière à masse négative ? Mathématiquement, il suffit de considérer que -1 = +(-1), et il est possible de l’intégrer à des calculs, et de la manipuler.
Autrement, par son comportement ! En particulier, son déplacement. De façon simple, et dans la Relativité Générale, les masses positives attirent tout, et les masses négatives repoussent tout. Et lorsqu’elles sont en présence les unes avec les autres, les masses négatives repoussent les masses positives, qui elles-mêmes les attirent ! Autrement dit, elles se courent après ! D’autre part, si ces masses sont égales et opposées, elles subissent un accroissement de vitesse et une accélération continue. C’est ce que l’on appelle « Paradoxe Runaway », et il viole le principe d’action-réaction selon lequel, d’après Newton, « tout corps A exerçant une force sur un corps B subit une force d’intensité égale, mais de sens opposé, exercée par le corps B. »
Et c’est la raison pour laquelle introduire des masses négatives dans l’Univers régi par la Relativité Générale a semblé impossible pendant plus de 50 ans.
Et comme le dit Jean-Pierre Petit dans une autre vidéo (celle dont vous trouverez le lien en fin d’article, page 4), « Est-il alors possible d’envisager un modèle où le principe d’action-réaction ne serait pas violé ? Pour cela, il faudrait que, placées dans un champ gravitationnel donné, créé par une certaine distribution de masses, positives ou négatives, les particules-témoins réagissent différemment selon leur signe. […] Il faut que le champ gravitationnel donne dans le premier membre (de l’équation d’Einstein) deux solutions, sous la forme de deux fonctions métriques qui engendreraient alors deux familles de courbes trajectoires différentes. C’est faisable si on envisage, non une seule équation, mais un système de deux équations de champs couplés ». Ce qui revient à considérer l’existence de deux univers !
L’idée d’univers opposés est d’abord avancée par le savant russe Andreï Sakharov. Dans sa géométrie, il oppose deux demi-univers énantiomorphes (symétriques « en miroir »), uniquement reliés par la singularité initiale du Big Bang.
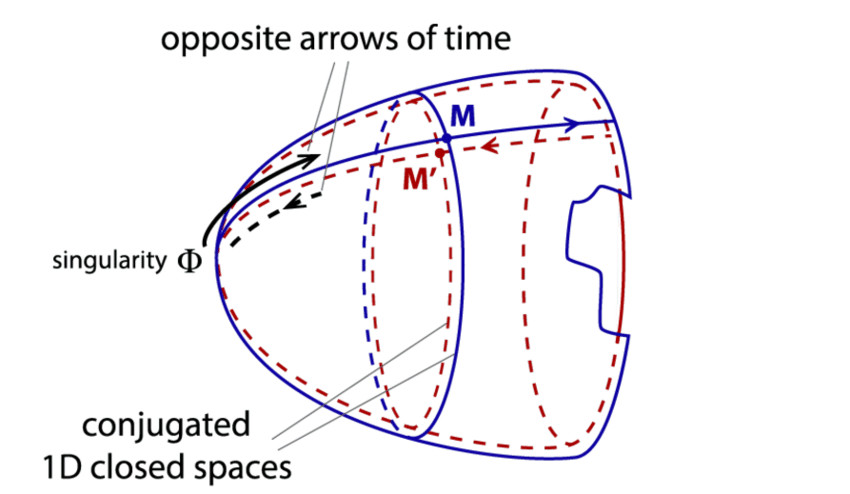
Dans la conception du Modèle Janus, le demi-univers jumeau est en quelque sorte replié, et son antimatière négative contient la matière de notre univers positif, assurant la cohésion de l’ensemble. Les deux univers sont cette fois-ci en interaction.
Dans les deux modèles, le temps de l’univers d’antimatière se déroule à l’envers du nôtre ! Il existe en effet une relation mathématique entre l’inversion des masses, celle de l’énergie, et celle du temps (mais pas du temps propre). Un lien vous orientera vers un contenu sur ce sujet à la page 4.
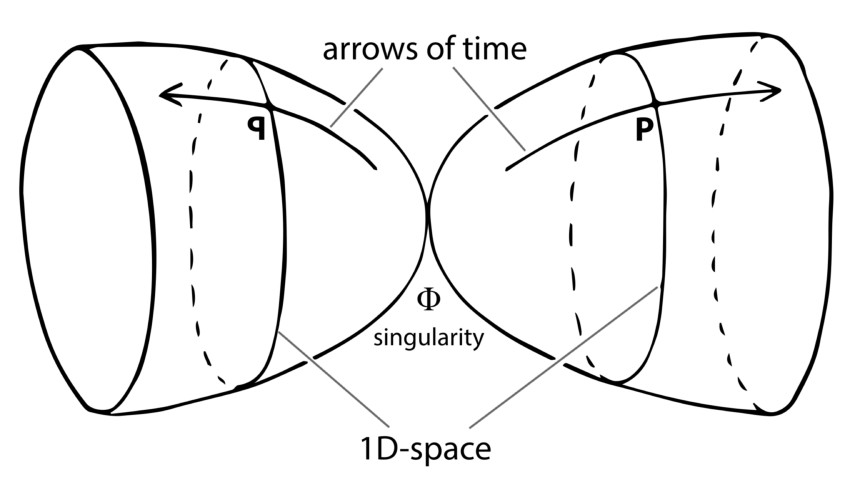
Géométries respectives du Modèle de Sakharov et du Modèle Janus. Source des images : Jean-Pierre. Petit.
Le Modèle Janus résout le Paradoxe Runaway sans violer le principe d’action-réaction, en insérant les masses négatives à l’intérieur des équations de la Relativité Générale. Selon Jean-Pierre Petit, l’ensemble concorde, mais d’une façon différente de celle que l’on envisageait jusqu’à présent : sans renier pour autant le modèle d’Einstein, il le complète d’un Univers Jumeau dans lequel les distributions de masses sont différentes, et où les lois physiques ne sont plus les mêmes !
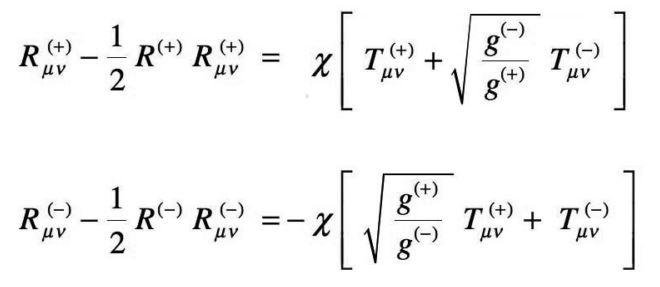
Équations du Modèle Janus par Jean-Pierre Petit. Le premier étage est celui de la Relativité Générale d’Einstein, le deuxième le complète en dessous avec des valeurs négatives.